7.2: Completely Randomized Design

After identifying the experimental unit and the number of replications that will be used, the next step is to assign the treatments (i.e. factor levels or factor level combinations) to experimental units. In a completely randomized design, treatments are assigned to experimental units at random. This is typically done by listing the treatments and assigning a random number to each. In the greenhouse experiment discussed in Chapter 1, there was a single factor (fertilizer) with 4 levels (i.e. 4 treatments), six replications, and a total of 24 experimental units (each unit a potted plant). Suppose the image below is the Greenhouse Floor plan and bench that was used for the experiment (as viewed from above). Top-down view of a greenhouse floor plan. A wall occupies the top of the diagram, and an open walkway occupies the bottom of the diagram. In the middle are 6 rows of 4 potted plants each.We need to be able to randomly assign each of the treatment levels to 6 potted plants. To do this, assign physical position numbers on the bench for placing the pots. The floor plan from Figure 1 above, with a number from 1 through 24 assigned to each of the plant locations. The plant spot at the top right corner is labeled 1, with numbers increasing by one from right to left within each row.

Using Technology

Minitab Example

Steps in Minitab In Minitab, this assignment can be done by manually creating two columns: one with each treatment level repeated 6 times (order not important) and the other with a position number 1 to \(N\), where \(N\) is the total number of experimental units to be used (i.e. \(N=24\) in this example). The third column will store the treatment assignment. 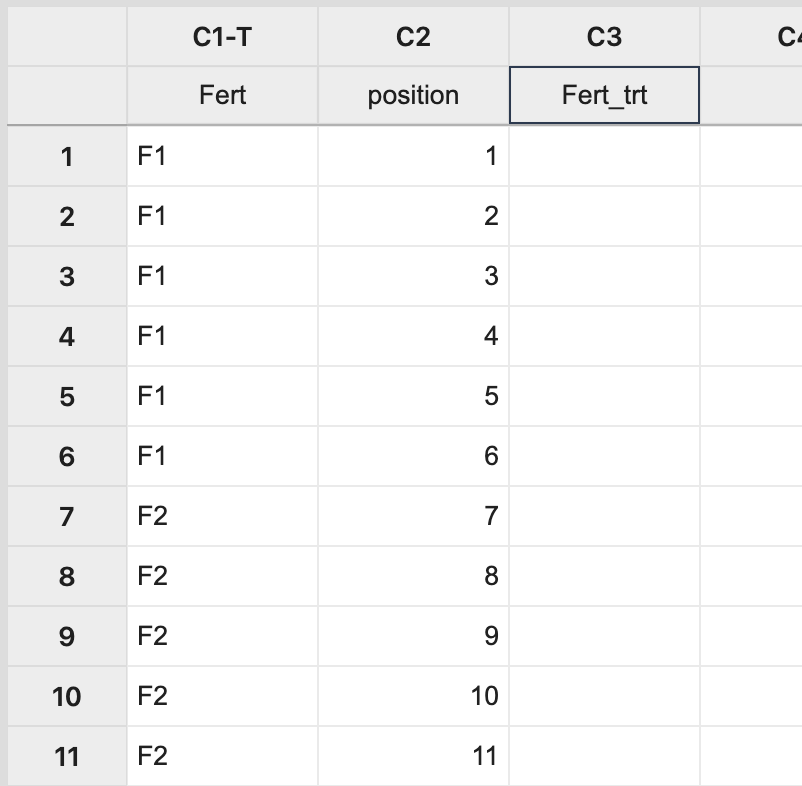In Minitab, Column 1 contains each fertilizer treatment repeated 6 times. Column 2 contains the plant positions, starting from 1. Column 3 will contain the treatment assignment for each plant position.Next, select Calc > Sample from Columns, fill in the dialog box as seen below, and click OK.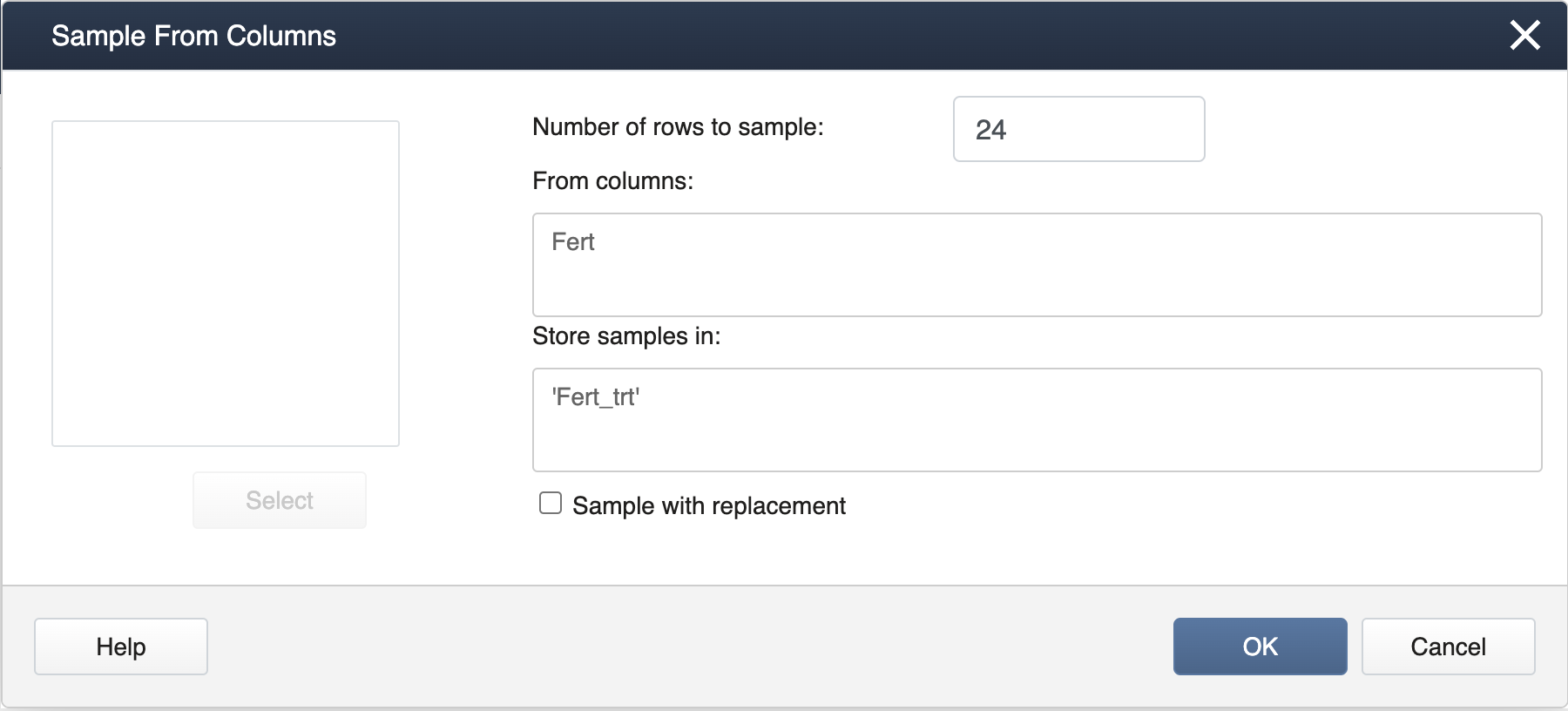 Minitab Sample from Columns pop-up window, with

Note!

Be sure to have the "Sample with Replacement" box unchecked so that all treatment levels will be assigned to the same number of pots, giving rise to a proper completely randomized design for a specified number of replicates.

This will result in a completely random assignment. 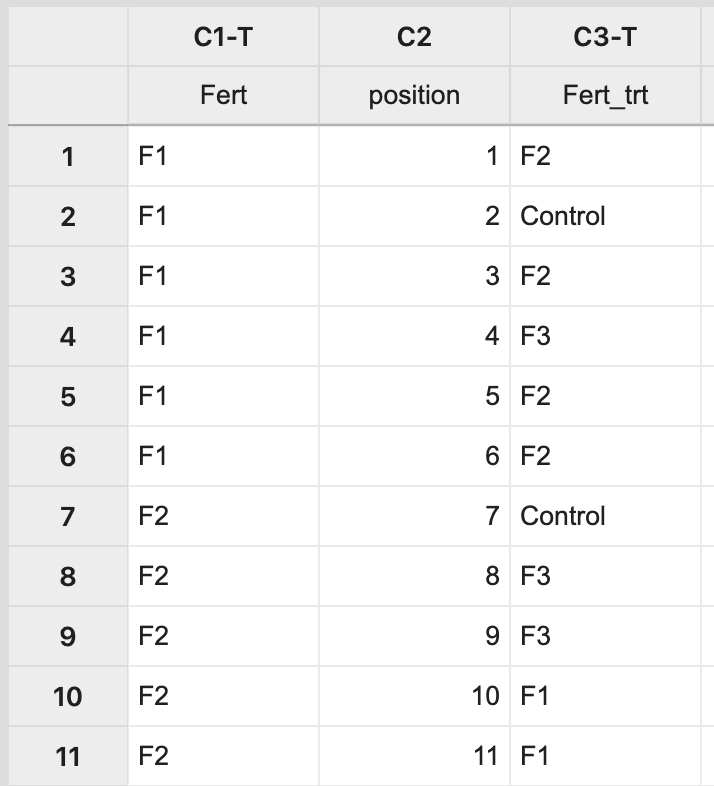The Minitab spreadsheet from Figure a1 above, with Column 3 filled with random fertilizer treatment assignments totaling 6 entries for each treatment type.This assignment can then be used to apply the treatment levels appropriately to pots on the greenhouse bench. Floorplan of the greenhouse with all plant positions labeled. Each plant is randomly assigned with one of the 4 fertilizer treatment levels, as represented by 4 differently covered tube icons, corresponding to the assignment in Column 3 in Figure a3 above.

SAS Example
Steps in SAS To make the assignments in SAS we can utilize the SAS surveyselect procedure as below: 
proc surveyselect data=greenhouse out=trtassignment outrandom method=srs samprate=1; run;

The output would be as below. In practice, it is recommended to specify a seed to ensure the results are reproducible.

Obs Fertilizer
1 F3
2 F2
3 Con
4 F2
5 F3
6 Con
7 F2
8 F2
9 F3
10 F1
11 F1
12 F3
13 F2
14 F1
15 F3
16 F3
17 F1
18 Con
19 Con
20 F2
21 Con
22 F1
23 Con
24 F1
R Example
Steps in R
Completely Randomized Design
To randomly assign treatment levels to each of our plants we can use the following commands: 
sample(treatment) [1] "F3" "F2" "F1" "F2" "F3" "F1" "Control" "F2" "F3" [10] "F3" "F2" "Control" "F3" "F1" "F1" "F2" "Control" "F2" [19] "F1" "Control" "F3" "Control" "Control" "F1"

This means that the first experimental unit will get Fertilizer 3, the second experimental unit will get Fertilizer 2, etc.

Randomized Complete Block Design

Obtain the block design. Load the greenhouse data and obtain the ANOVA table. To obtain the block design we can use the following commands:

library(blocksdesign) block_design# obs block plant treatment # 1 1 1 1 4 # 2 2 1 2 1 # 3 3 1 3 3 # 4 4 1 4 2 # 5 5 2 1 1 # 6 6 2 2 4 # 7 7 2 3 3 # 8 8 2 4 2 # 9 9 3 1 3 # 10 10 3 2 1 # 11 11 3 3 4 # 12 12 3 4 2 # 13 13 4 1 1 # 14 14 4 2 4 # 15 15 4 3 2 # 16 16 4 4 3 # 17 17 5 1 3 # 18 18 5 2 2 # 19 19 5 3 1 # 20 20 5 4 4 # 21 21 6 1 2 # 22 22 6 2 1 # 23 23 6 3 4 # 24 24 6 4 3

To load the greenhouse data and obtain the ANOVA table ( lmer() and aov( )) we use the following commands:

setwd("~/path-to-folder/") greenhouse_RCBD_data read.table("greenhouse_RCBD_data.txt",header=T) attach(greenhouse_RCBD_data) library(lmerTest) library(lme4) greenhouse_RCBD_anova<-lmer(Height ~ Fertilizer + (1 | factor(Block)),greenhouse_RCBD_data) anova(greenhouse_RCBD_anova) #Type III Analysis of Variance Table with Satterthwaites method # Sum Sq Mean Sq NumDF DenDF F value Pr(>F) #Fertilizer 251.44 83.813 3 15 162.96 1.144e-11 *** #--- #Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 greenhouse_RCBD_anova1#Error: factor(Block) # Df Sum Sq Mean Sq F value Pr(>F) #Residuals 5 53.32 10.66 #Error: Within # Df Sum Sq Mean Sq F value Pr(>F) #Fertilizer 3 251.44 83.81 163 1.14e-11 *** #Residuals 15 7.72 0.51 #--- #Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
For comparison the ANOVA table for the completely randomized design is given below: 
greenhouse_CRD_anova# Df Sum Sq Mean Sq F value Pr(>F) #Fertilizer 3 251.44 83.81 27.46 2.71e-07 *** #Residuals 20 61.03 3.05 #--- #Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 detach(greenhouse_RCBD_data)

This page titled 7.2: Completely Randomized Design is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Penn State's Department of Statistics.

  1. Back to top